数模mooc笔记
NIM游戏(数论模型)
游戏描述
- 现有n堆硬币,每堆数量一定
- 两人轮流取硬币,每次只能从其中一堆中取,每次取至少一枚
- 取到最后一枚硬币的一方获胜
 ### 必胜策略
### 必胜策略 



秘密共享(数论与代数模型)
描述:
- 安全门上安装多把锁,所有锁同时打开时安全门才能打开。每人拥有部分锁的钥匙,每把钥匙只能打开一把锁,一把锁可以配多把钥匙。
### 组合方法
 #### 推广
#### 推广 

Shamir门限机制
密码学
- 秘密共享(secret sharing) 将秘密分成若干份,分发给不同的用户。用户特定子集共同提供各自的份额,才能重构初始秘密。
- 门限机制(threshold scheme) 在n人之间共享秘密,其中任意
个人可求出秘密,任意t-1个人无法求出秘密。 #### Shamir门限机制(t,n) 

 what↑ ### 中国剩余定理
what↑ ### 中国剩余定理 


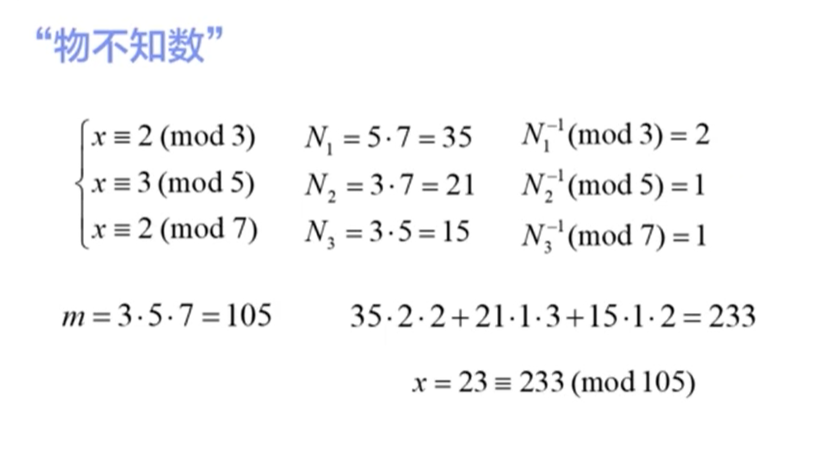 ### Asmuth-Bloom门限机制
### Asmuth-Bloom门限机制




蛛网模型与Cournot模型(函数与数列模型)
商品价格与均衡

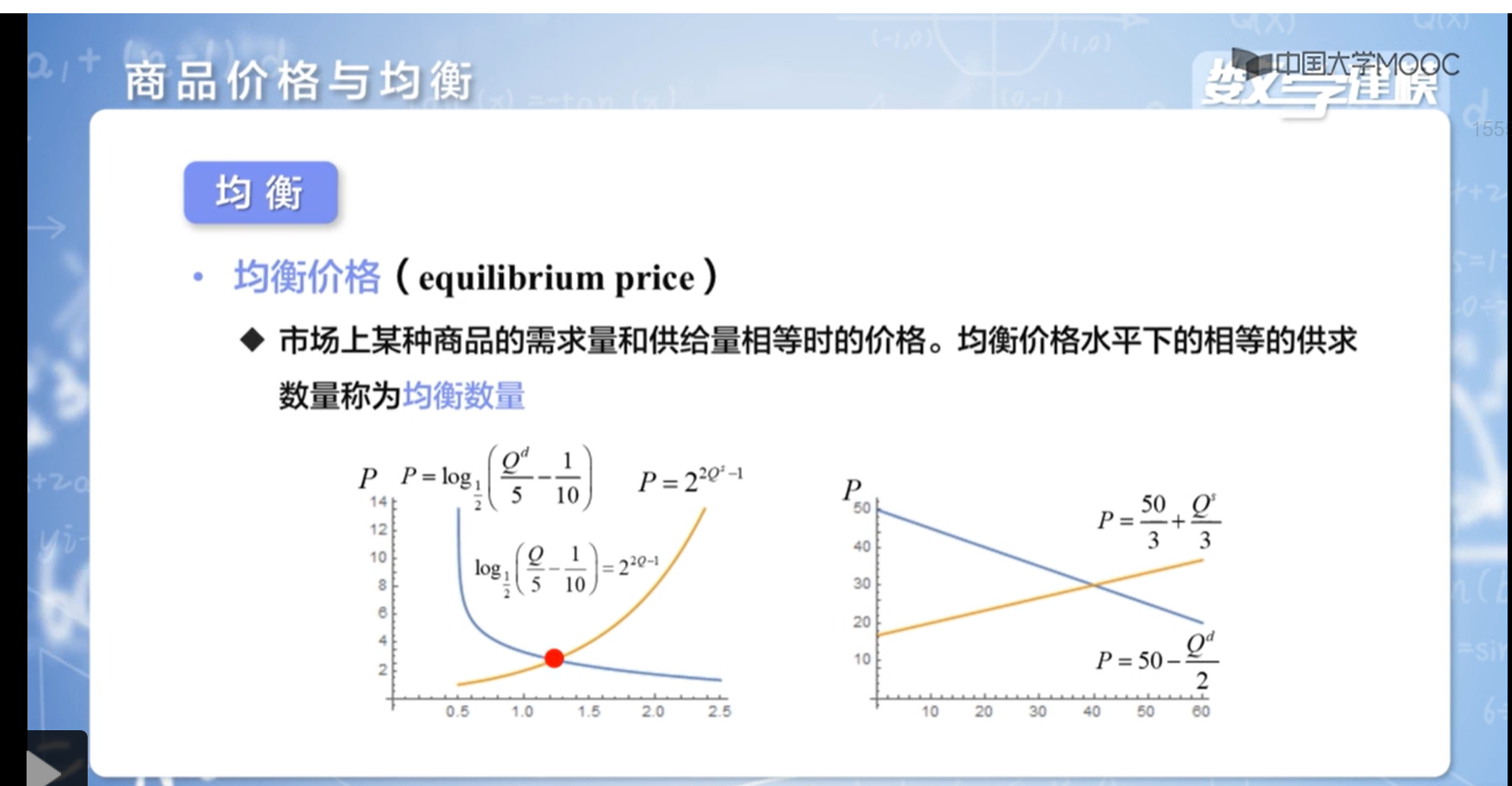
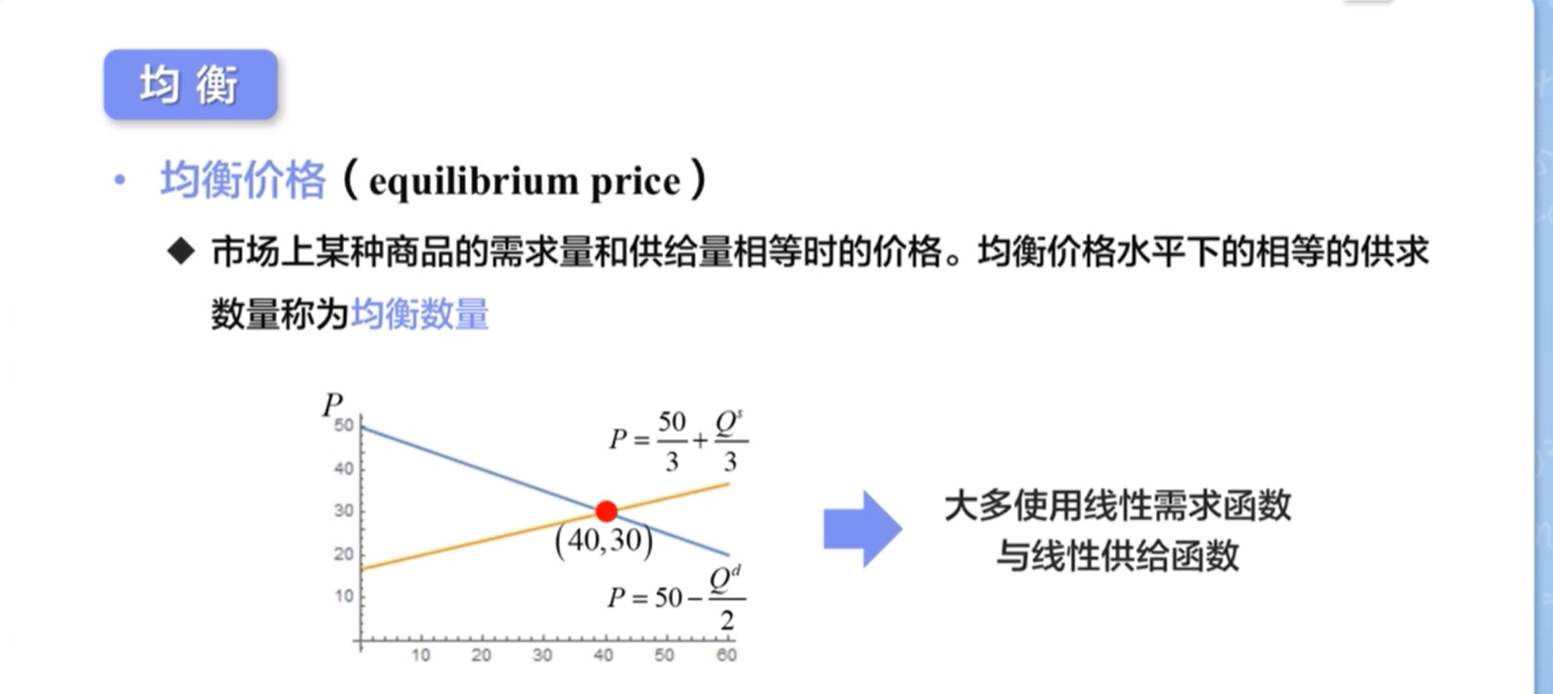
蛛网模型

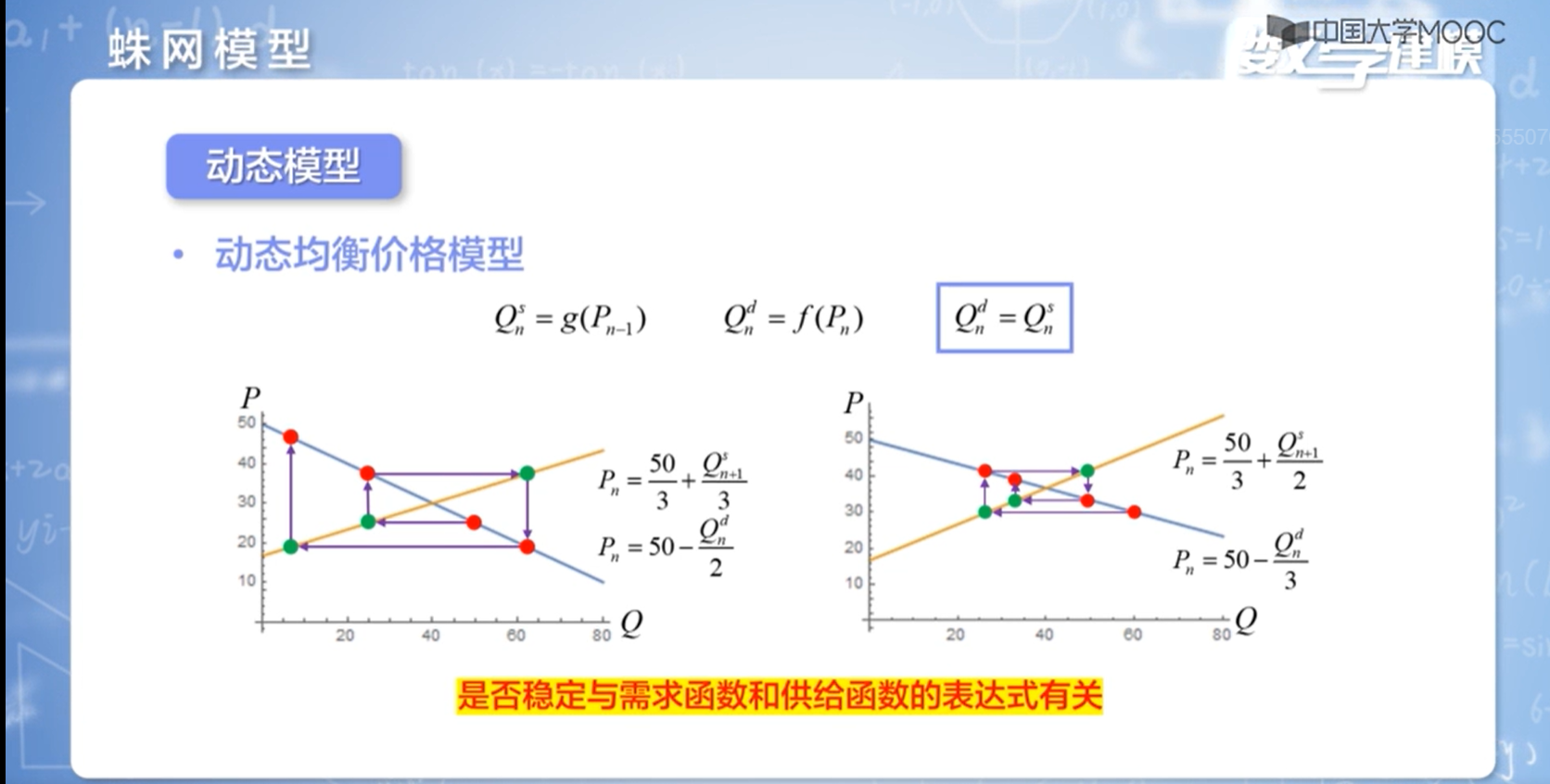


 即收敛要求商品价格上涨时,供给量的增加量,应小于需求量的减小量
即收敛要求商品价格上涨时,供给量的增加量,应小于需求量的减小量 

差分方程


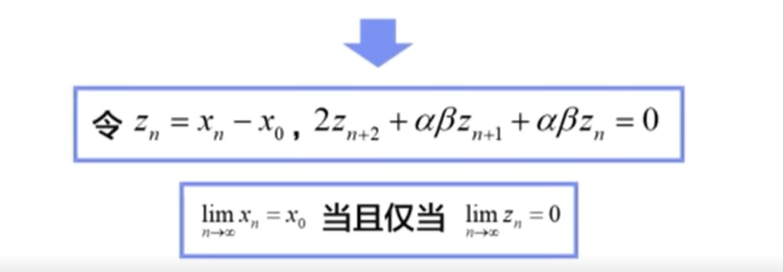 #### 差分
#### 差分 
 #### 含有未知函数的有限差分的方程 -
#### 含有未知函数的有限差分的方程 - 




Cournot模型(古诺模型)


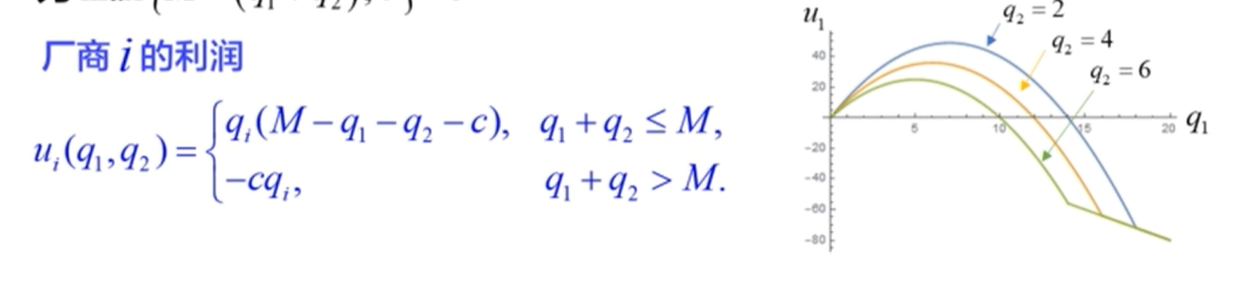

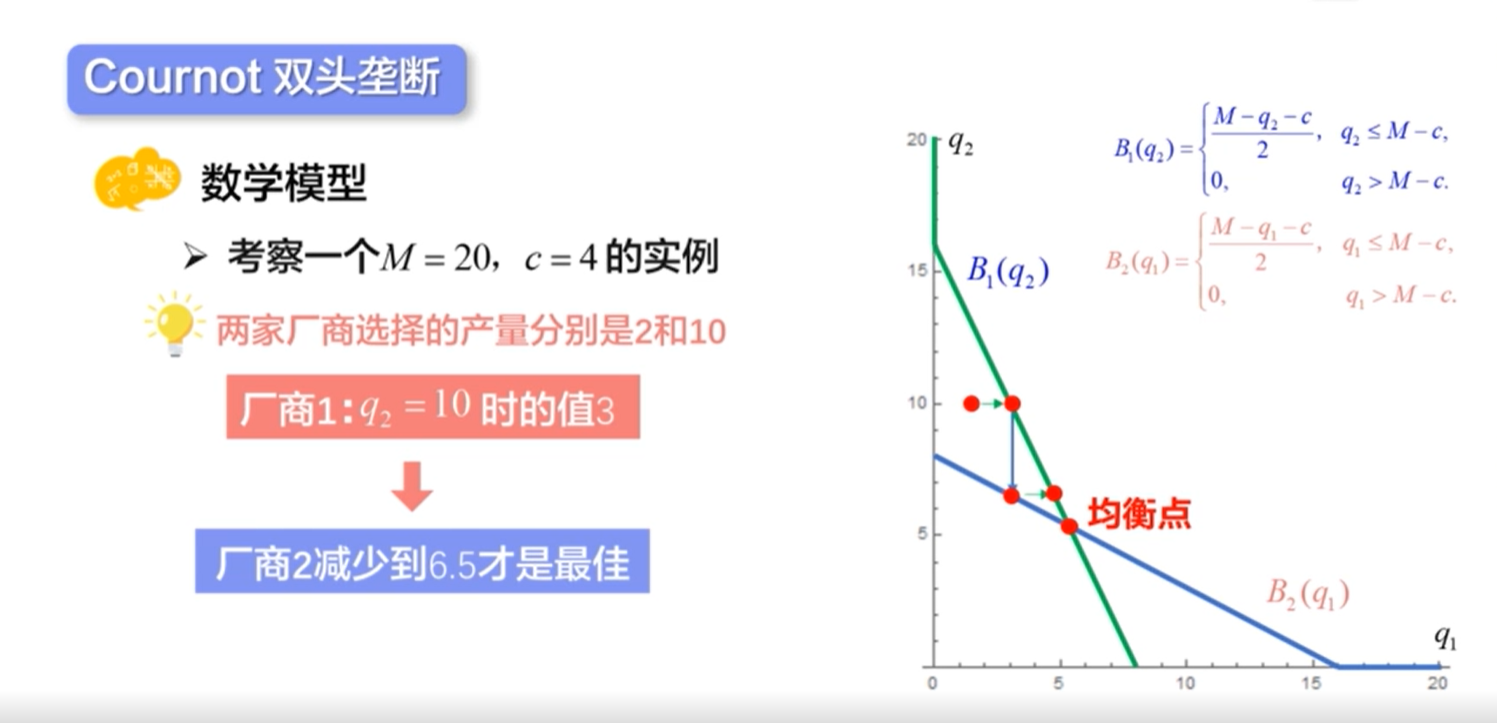

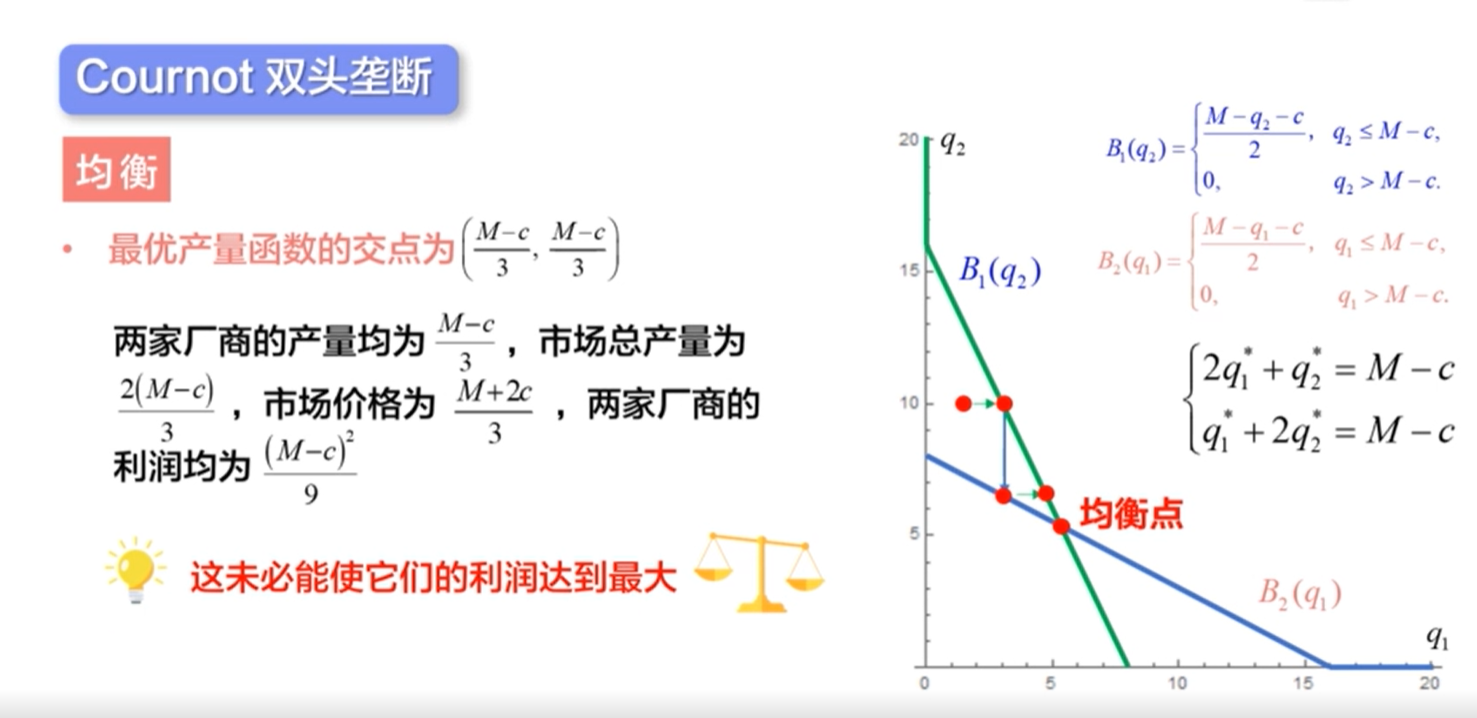





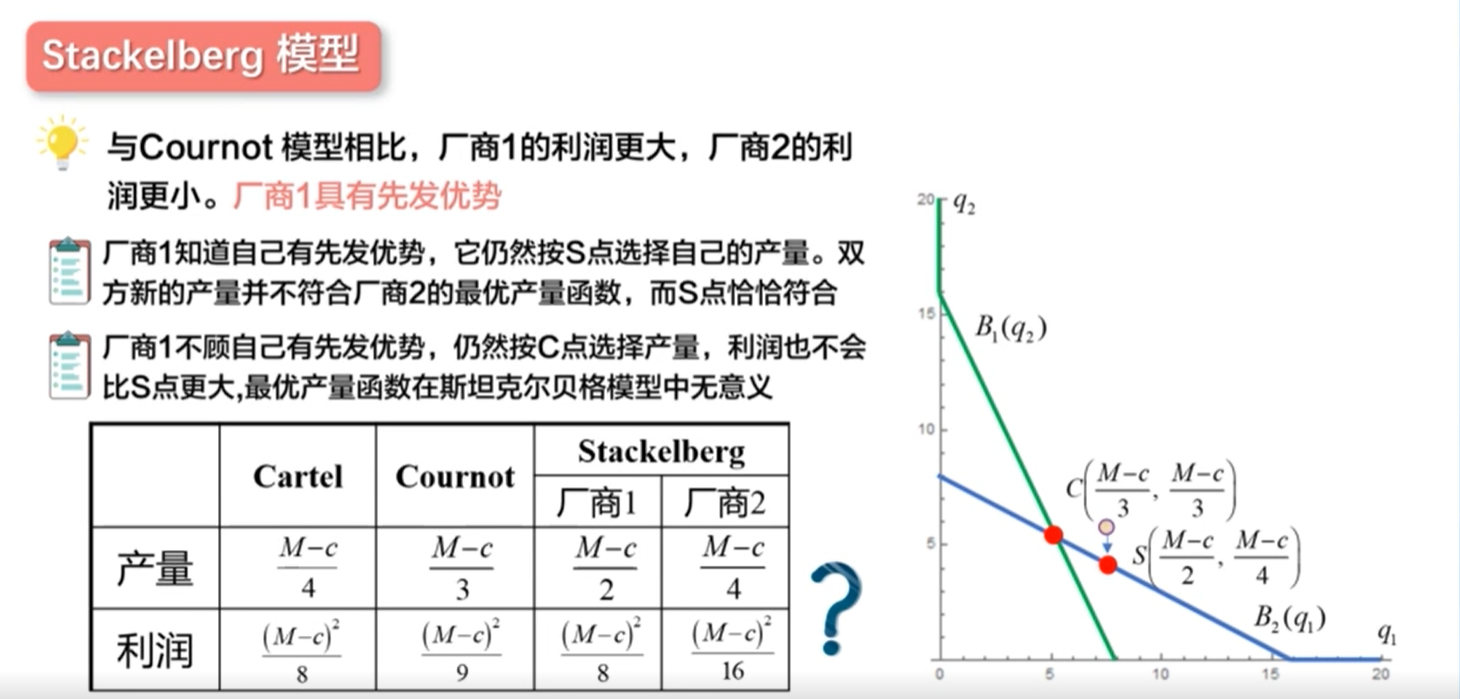
Bertrand模型

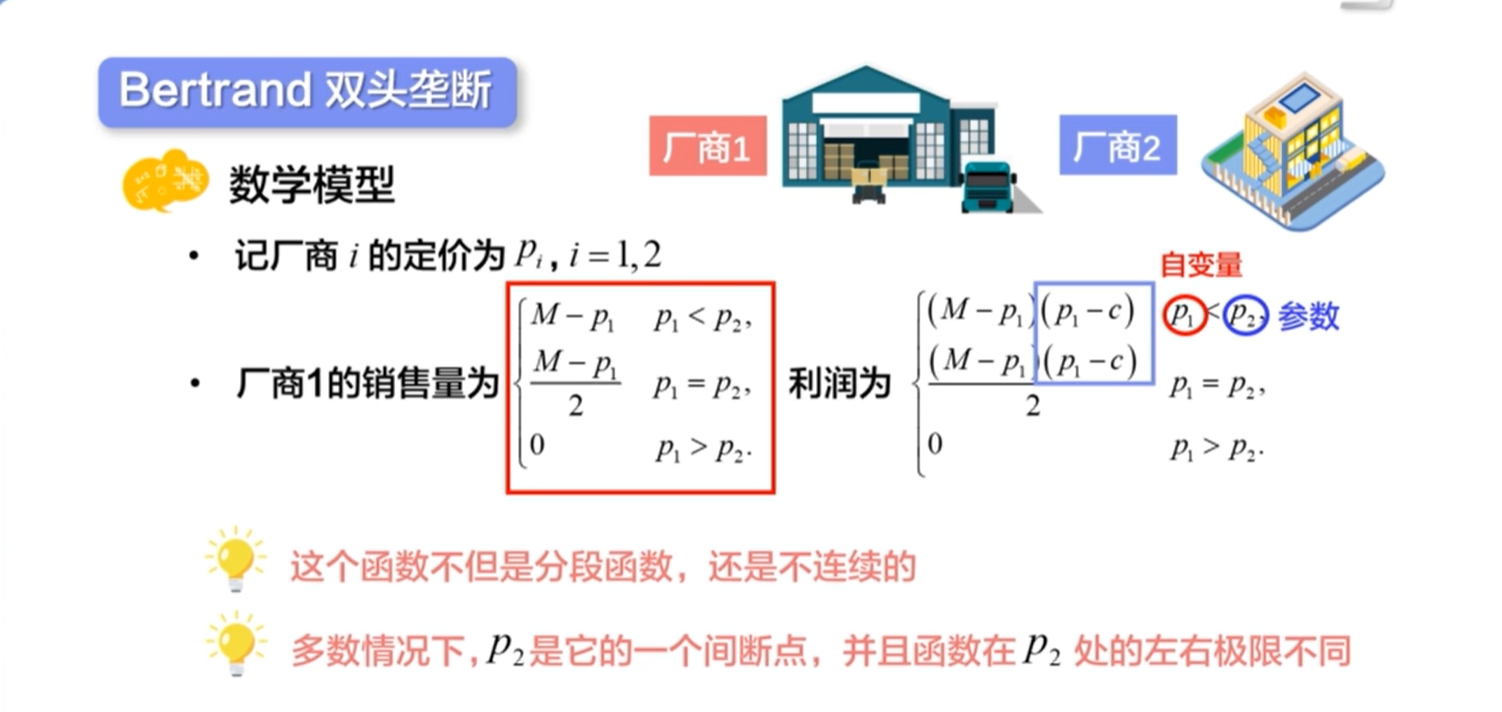
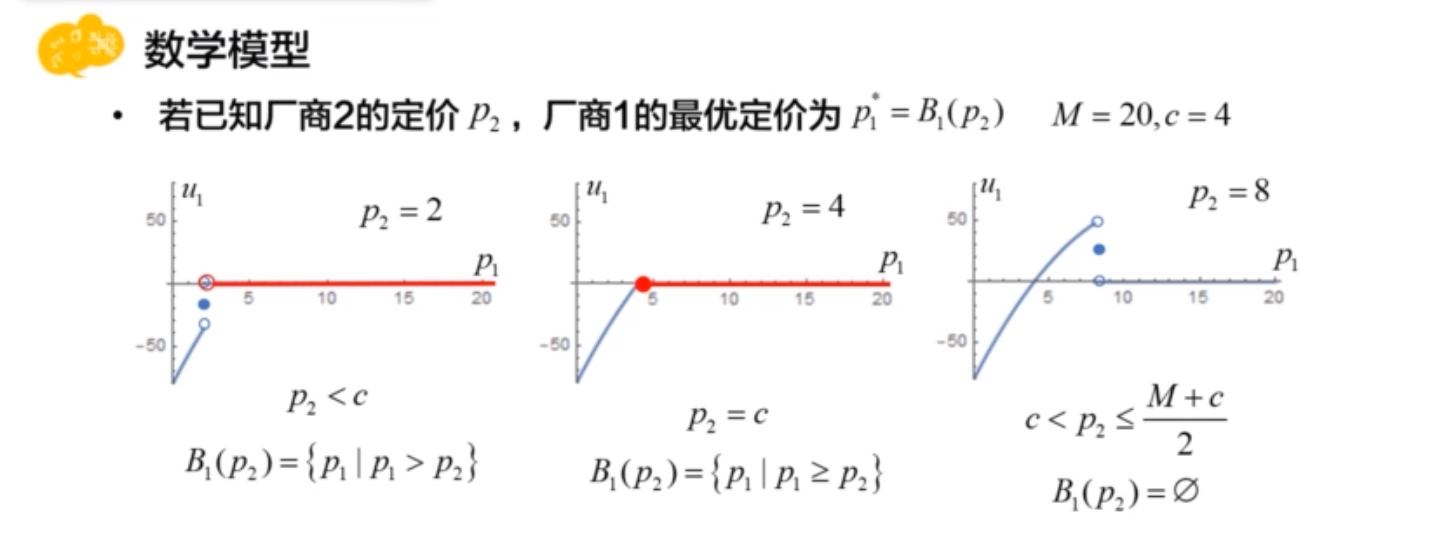

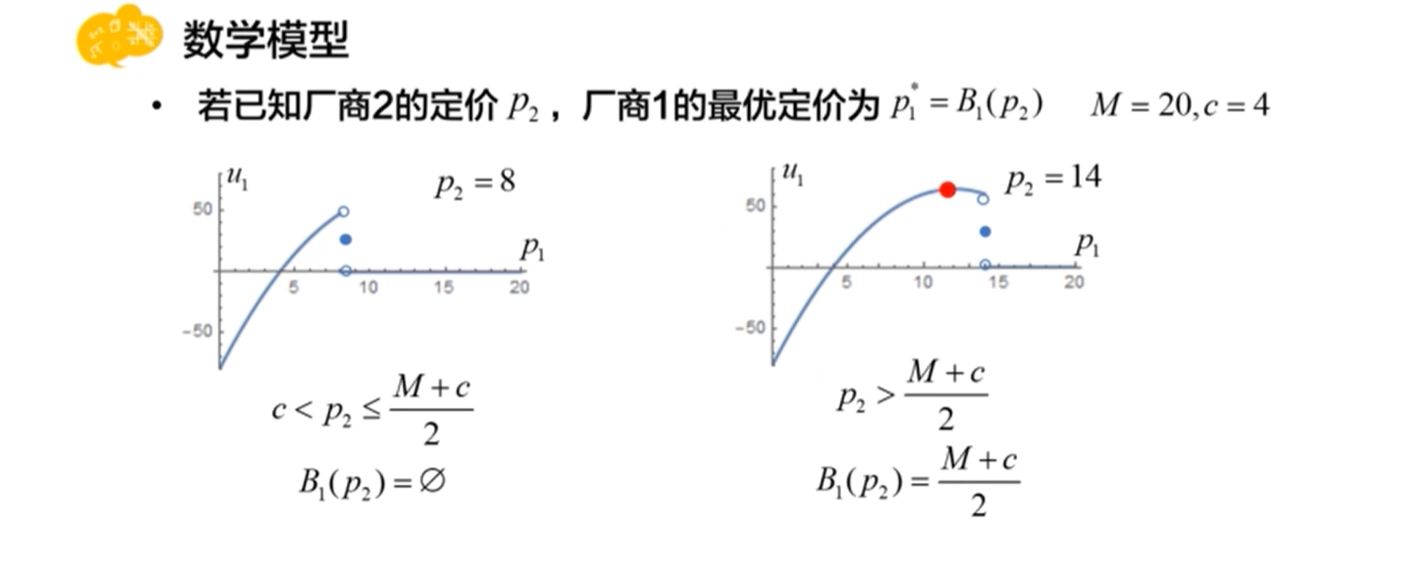
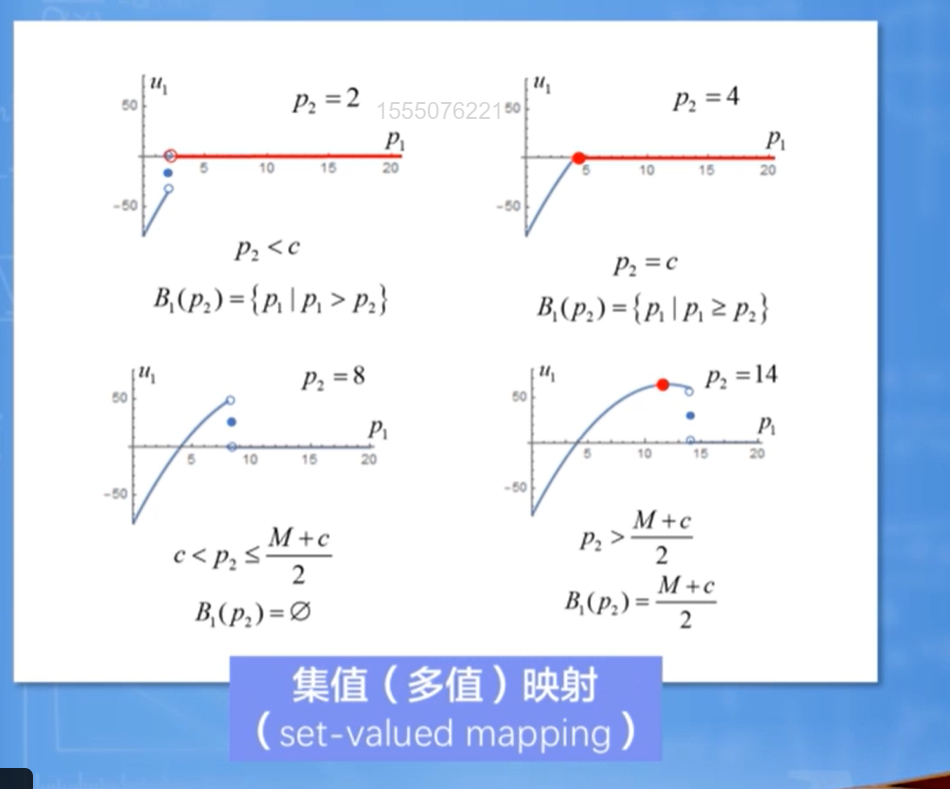

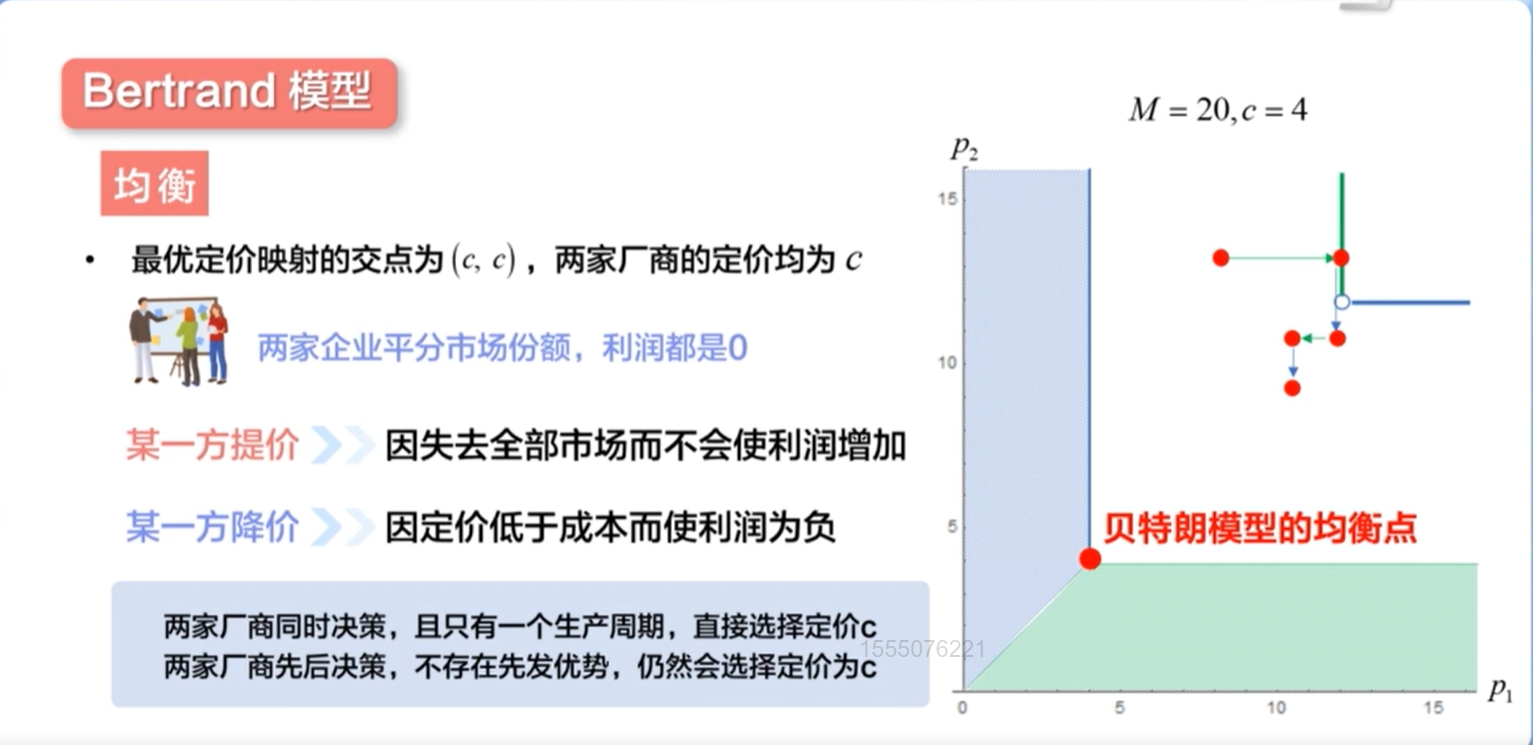



Monty Hall问题(概率模型)
疾病检测
- 疾病监测方法的性能指标
- 灵敏度(sensitivity)p 患病者被检测为阳性的概率
- 特异度(specificity)q 未患病者被检测为阴性(negative)的概率
- 两者不能相互替代
- 被检测为阳性的情况下患病的概率
记A为患病,B为检测结果为阳性:灵敏度
,特异度 设疾病的发病率为r 
Monty Hall问题的基本形式(蒙蒂霍尔问题)
观众参与的竞猜游戏 #### 补充设定: - 假设主持人知道汽车所在的位置 - 竞猜者选择后,主持人打开的门既不是竞猜者选择的,也不是后面有汽车的。 - 有时可能有两扇门符合上面的要求,比如竞猜者初次选择的门后就是汽车,那么另外两扇门后都是山羊。主持人以相等的概率选择其中一扇打开。
原问题中,汽车的位置是事先固定的。竞猜者在没有任何信息的情况下,选择三扇门的概率都是1/3。
等价假设
- 假设竞猜者初次选择1号门,汽车位于1、2、3号门后的概率相同。
- 如果汽车在1号门后,主持人以相等的概率打开2号门或3号门中的其中一扇
- 汽车在2号门后,主持人只能打开3号门
- 汽车在3号门后,主持人只能打开2号门
- 若竞猜者不改变选择,则获得汽车的概率为1/3
- 若竞猜者改变选择,则获得汽车的概率为2/3
- 竞猜者获得汽车的概率是原来的两倍

数学推导
- 假设竞猜者初次选择1号门 记
- 假设主持人打开2号门 记
- 主持人打开2号门这一事件发生情况下,获得汽车这一事件的条件概率
- 若竞猜者不改变选择,获得汽车的概率为
- 若竞猜者改变选择,选择三号门,获得汽车的概率为
- 若竞猜者不改变选择,获得汽车的概率为
- 汽车在不同门后,主持人打开2号门的条件概率是不同的:
- 汽车在1号门后,主持人只有一半的可能打开2号门
- 汽车在3号门后,主持人一定打开2号门
Monty Hall问题的推广
另一种假设
- 竞猜者选择之后,主持人以相同的概率打开其中的一扇。
- 主持人打开的门后是汽车 游戏以另一种方式结束,不在我们的讨论范围之内
- 主持人打开的门后是山羊 记
- 若竞猜者不改变选择,获得汽车的概率为
- 若竞猜者改变选择,选择三号门,获得汽车的概率为
- 主持人不知道汽车在哪里,他的行为就不会提供有用的信息
Monty Hall问题的变形
- 多扇门的蒙蒂霍尔问题
- 有
- 当至少有三扇门还未打开时,竞猜者选择其中一扇未打开的门,主持人以相同概率打开竞猜者未选择且后面是山羊的门中的任意一扇,并允许竞猜者改变之前的选择。继续上述过程直至只有两扇门还未打开
- 有
- 多扇门、多辆车的蒙蒂霍尔问题
- 有
- 竞猜者选择其中一扇门后,主持人以相同概率打开了其他
- 有
- 多扇门、多种奖品的蒙蒂霍尔问题
- 有
- 竞猜者选择其中一扇门后,主持人以相同概率打开了其他
- 有
安全观演(几何模型)
观演距离问题
安全观演问题条件
广场某处正在进行一场露天表演,若干人先后到达附近并选择一个地点观看表演
##### 观众选择地点的要求: - 与舞台中心的距离不小于L -
与之前到达的任一观众的距离不小于r -
在满足上述要求的情况下,观众选择与舞台中心距离最近的某个点 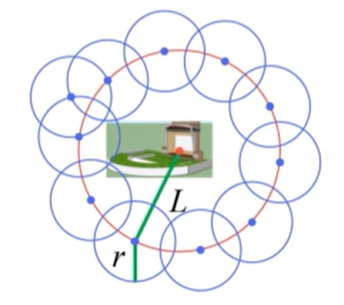
观众选择地点的方式:
- 有引导:观众在工作人员引导下到达满足要求的地点
- 无引导:观众自行选择满足要求的地点
观演距离
- 求第n个到达的观众与舞台中心的距离
观演距离
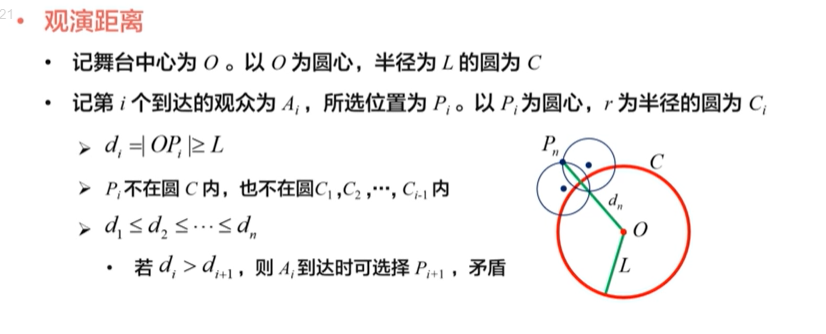


无遮观演
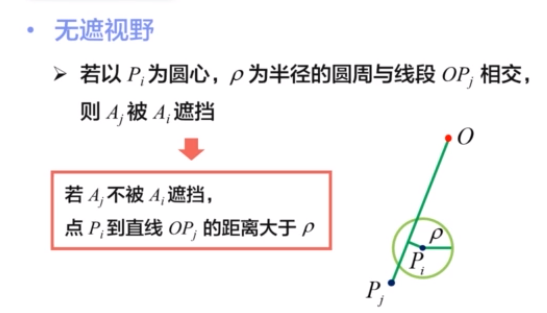


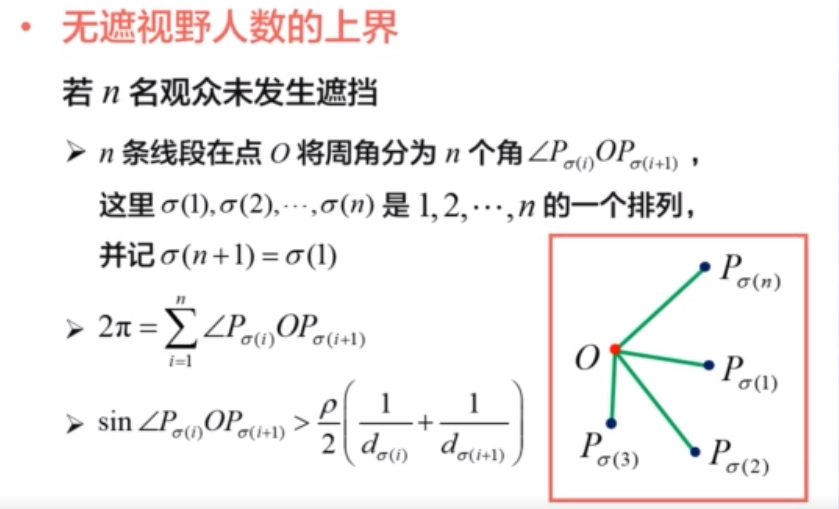
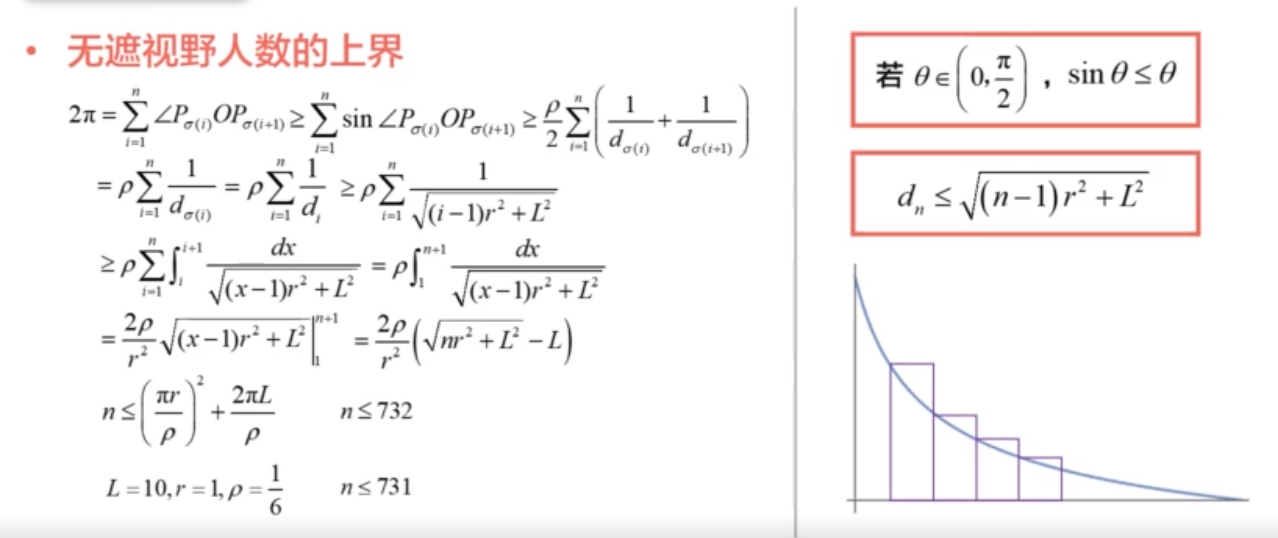
评论
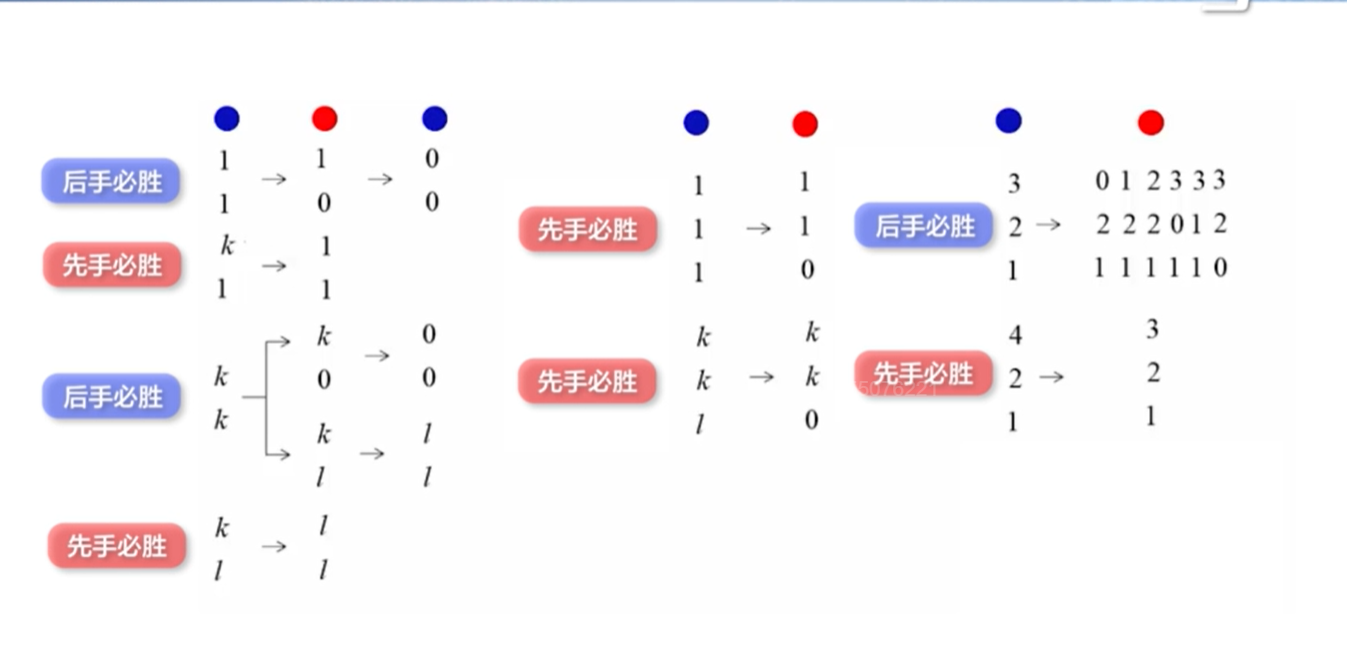 ### 必胜策略
### 必胜策略 
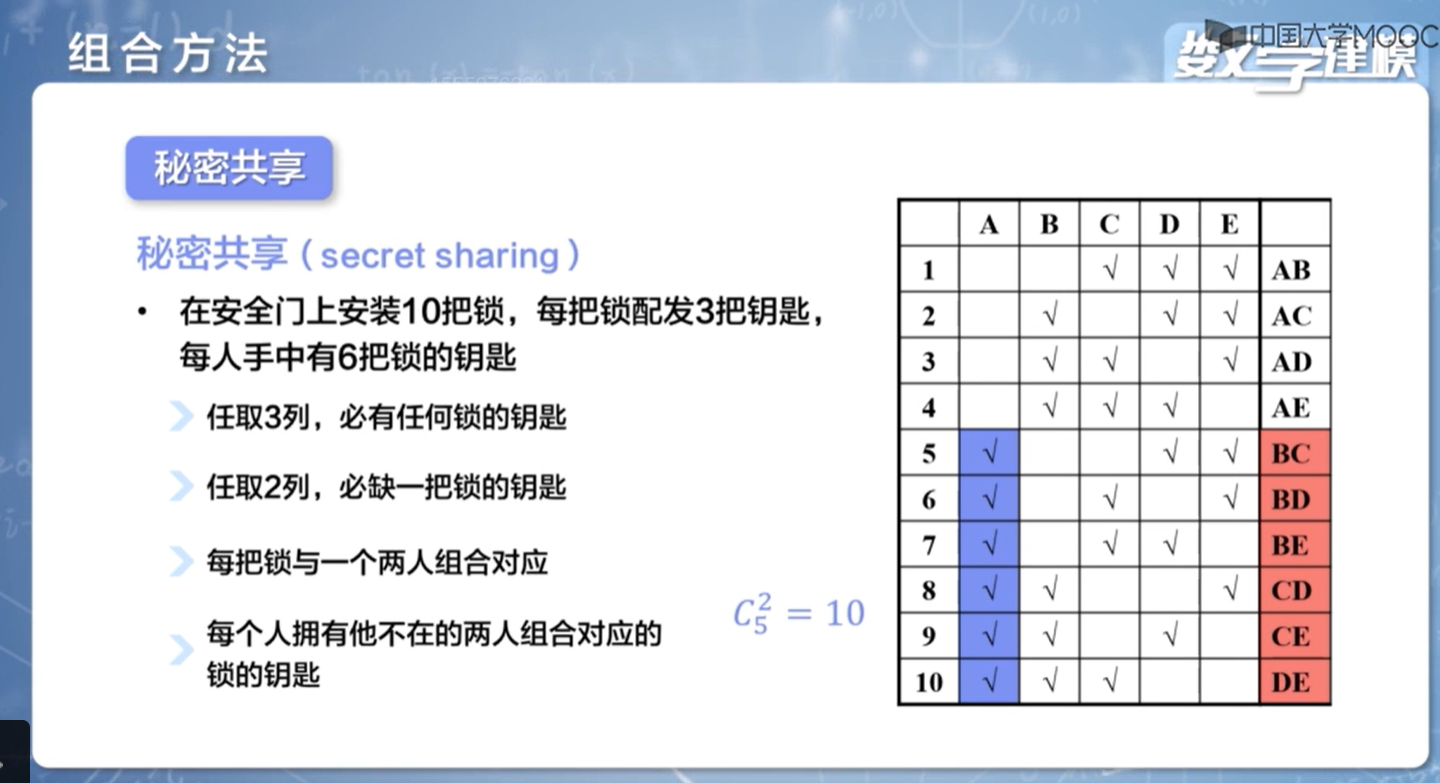 #### 推广
#### 推广 


 what↑ ### 中国剩余定理
what↑ ### 中国剩余定理 

