电网络分析笔记

课件、图片来源：浙江大学-孙盾-电网络分析

1 双口网络

1.1 定义

四端(钮)网络: 具有四个端钮的网络。

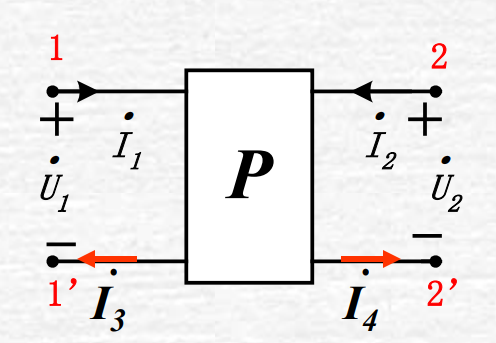
双口网络: 四个端钮两两成对，每一对端钮的电流必须是一进一出相等。这样对外呈现两个端口特性的网络称为二端口网络，或称为双口网络。

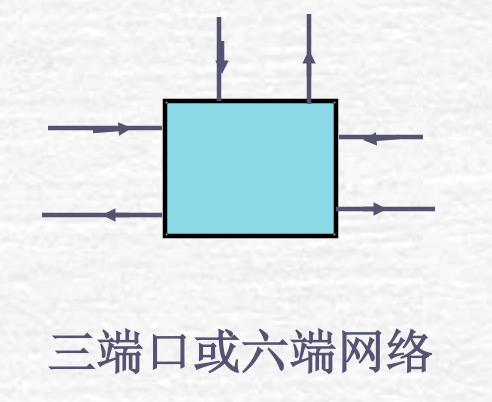
1.2 分类

（1） - 线性：由线性元件组成的双口网络称为线性双口网络 - 非线性：否则称为非线性双口网络（2） - 可逆：满足互易定理的双口网络称为可逆双口网络 - 不可逆：否则称为不可逆双口网络（3） - 对称：旋转180°，两电路重合的双口网络称为对称双口网络 - 不对称：否则称为不对称双口网络

1.3 双口网络的参数

Y参数（短路参数）

称为Y参数矩阵或短路参数矩阵 $短路时端口的入端导纳短路时端口间的转移导纳短路时端口间的转移导纳短路时端口的入端导纳$

如果网络可逆，不含受控源的双口网络满足互易定理，必定为可逆双口网络；
如果网络对称， $，$

Z参数

称为Z参数矩阵或开路参数矩阵

$开路时端口的入端阻抗开路时端口间的转移阻抗短路时端口间的转移导纳短路时端口的入端导纳$

如果网络可逆，
如果网络对称， $，$

T参数

：T参数矩阵或称传输参数矩阵 $开路时的转移电压比开路时的端口间的转移导纳短路时的端口间的转移阻抗短路时的转移电流比$

如果网络可逆，
如果网络对称，
入端阻抗：

H参数

：H参数矩阵或称混合参数矩阵

B参数

逆传输参数矩阵

G参数

逆混合参数矩阵

1.4 互易双口网络的等效电路

只有3个参数

T型等效电路（可逆双口网络）

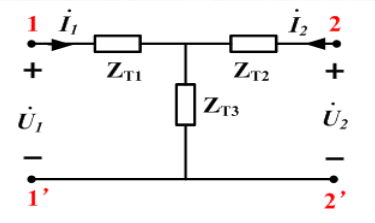
Z参数表示

T参数表示

型等效电路

##### T参数表示

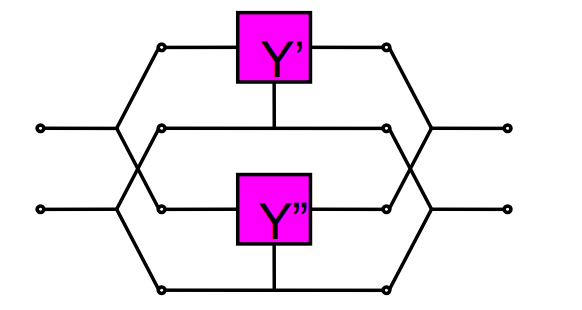
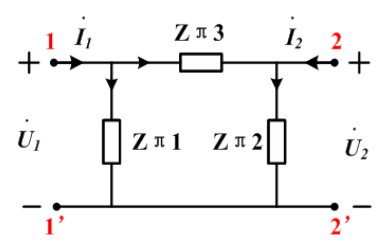
Y参数表示（可逆双口网络）

1.5一般双口网络的等效电路

有很多，在此列出两种

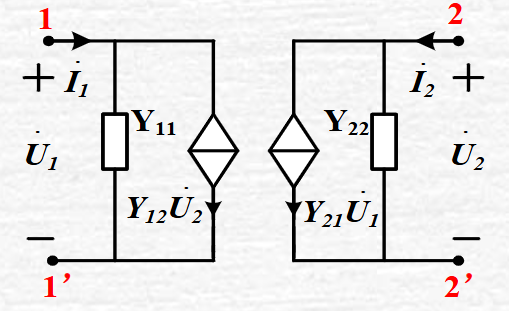
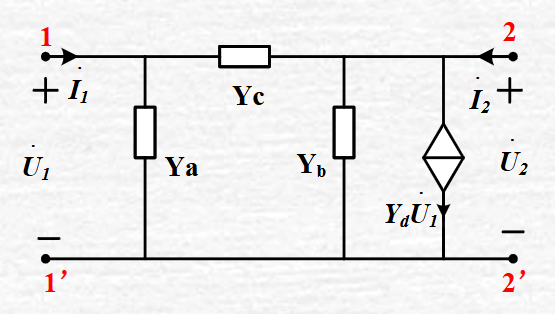
1.6 双口网络的连接

串联

输入端口串联输出端口串联 注意有效性问题

(1)有效串联时，串联后复合双口网络Z参数矩阵等于两串联双口网络Z参数矩阵相加。可推广到n端口串联。

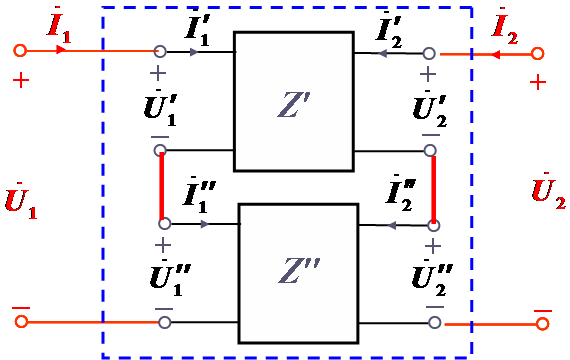
Z参数有效连接时：

串联电流相等：
则
即 (2)具有公共端的双口网络，将公共端串联时不会破坏端口条件

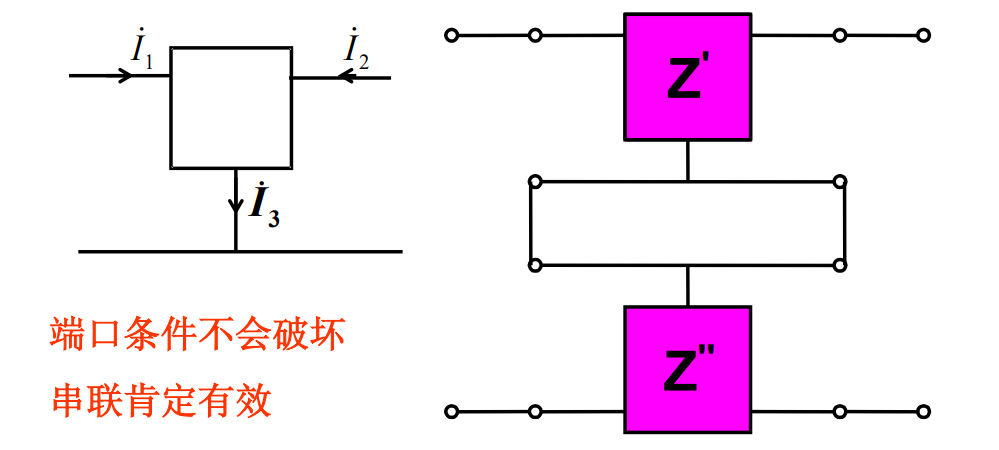
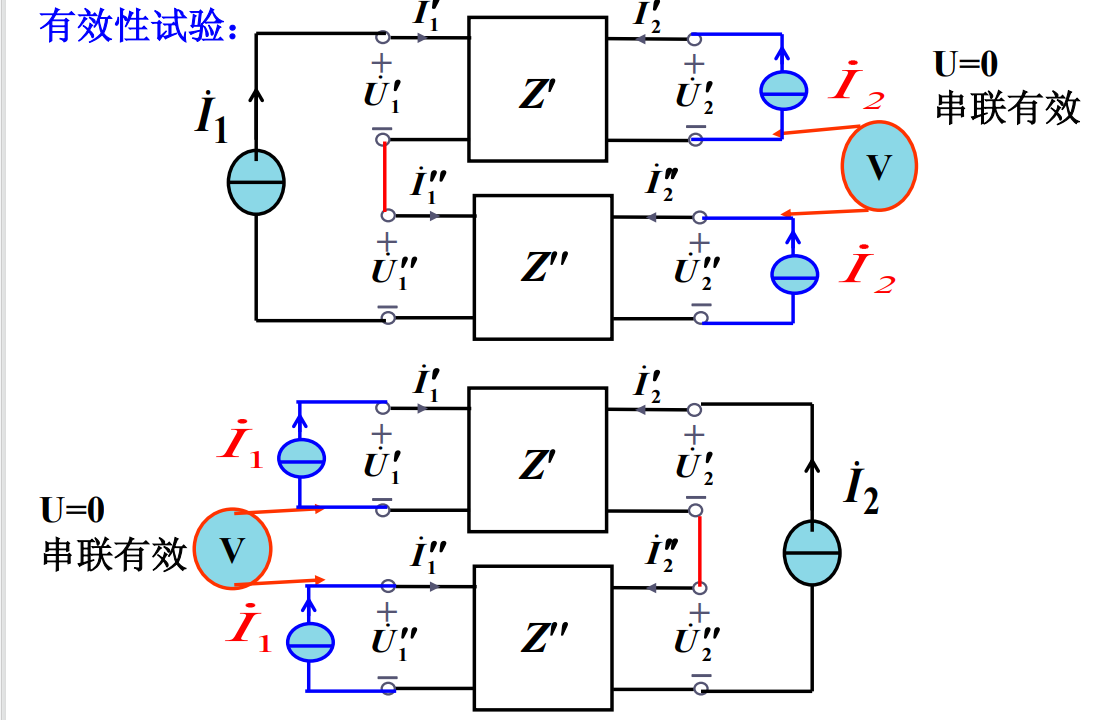
(3)有效性试验

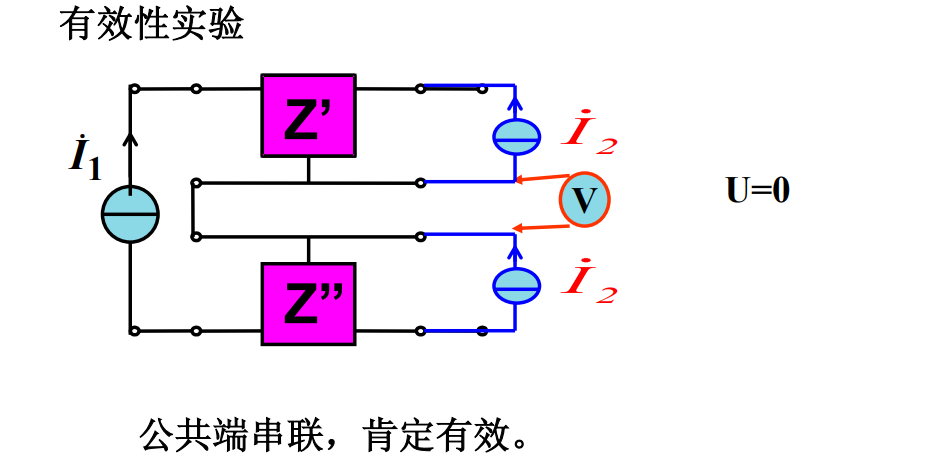
并联

输入端口并联，输出端口并联 注意有效性问题

(1)有效并联时，并联后所得复合双口网络的Y参数矩阵等于两个双口网络Y参数矩阵相加

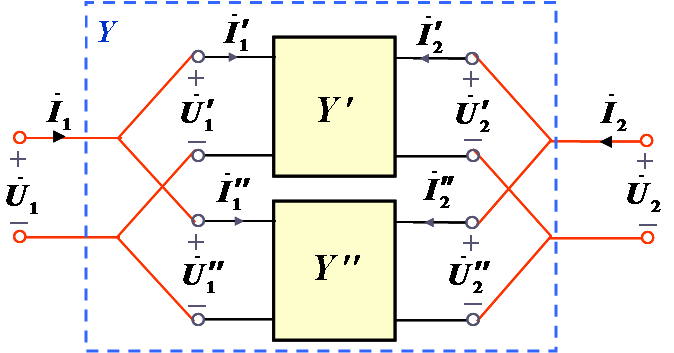
Y参数有效连接时：

$有效联接时：$

则

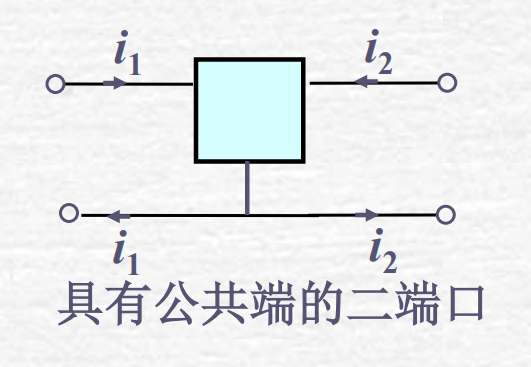
具有公共端的二端口，将公共端并在一起时不会破坏端口条件

(3)有效性试验

有公共接线的双口网络必满足并联有效性条件，例如两个三端网络并联必满足有效性条件。

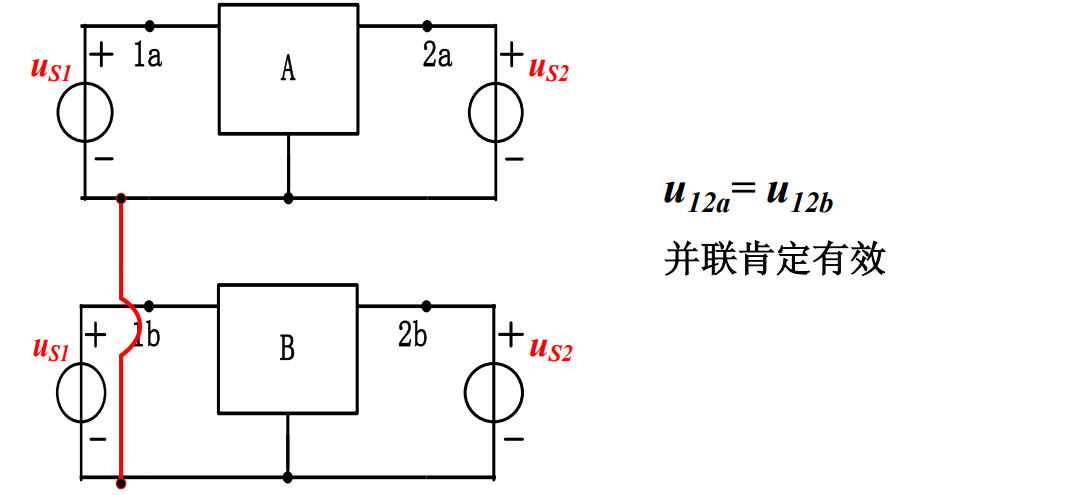
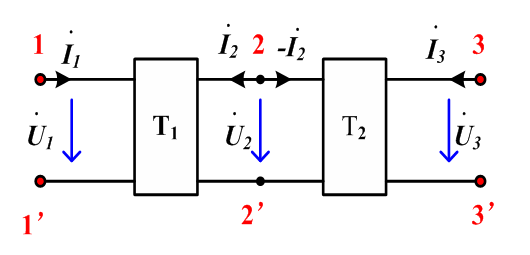
级联

无有效性问题（总有效） 前一级双口网络的输出作为后一级双口网络的输入，如此连接的方式称为级联。

1.7双口网络的应用

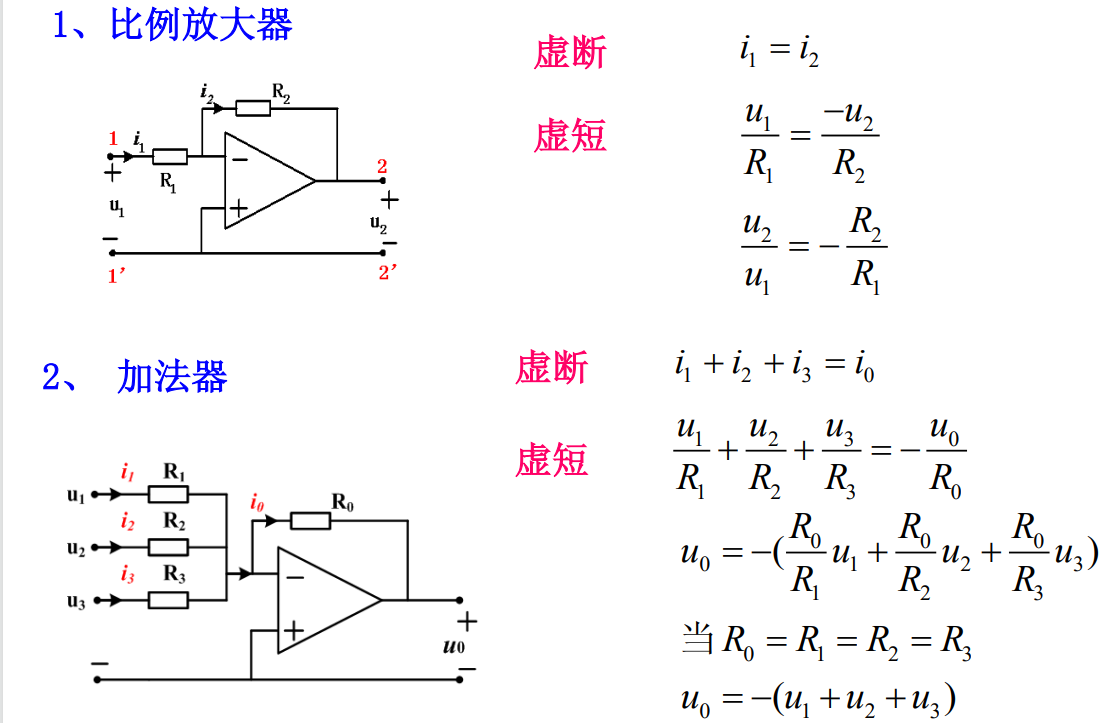
1.7.1 运算放大器

集成运算放大器是非常重要的一种集成电路，它的应用十分广泛。主要应用在模拟信号的运算、放大、信号产生、变换及检测等电路中，是通过半导体集成工艺制成的一种高增益、直接耦合式多级放大器。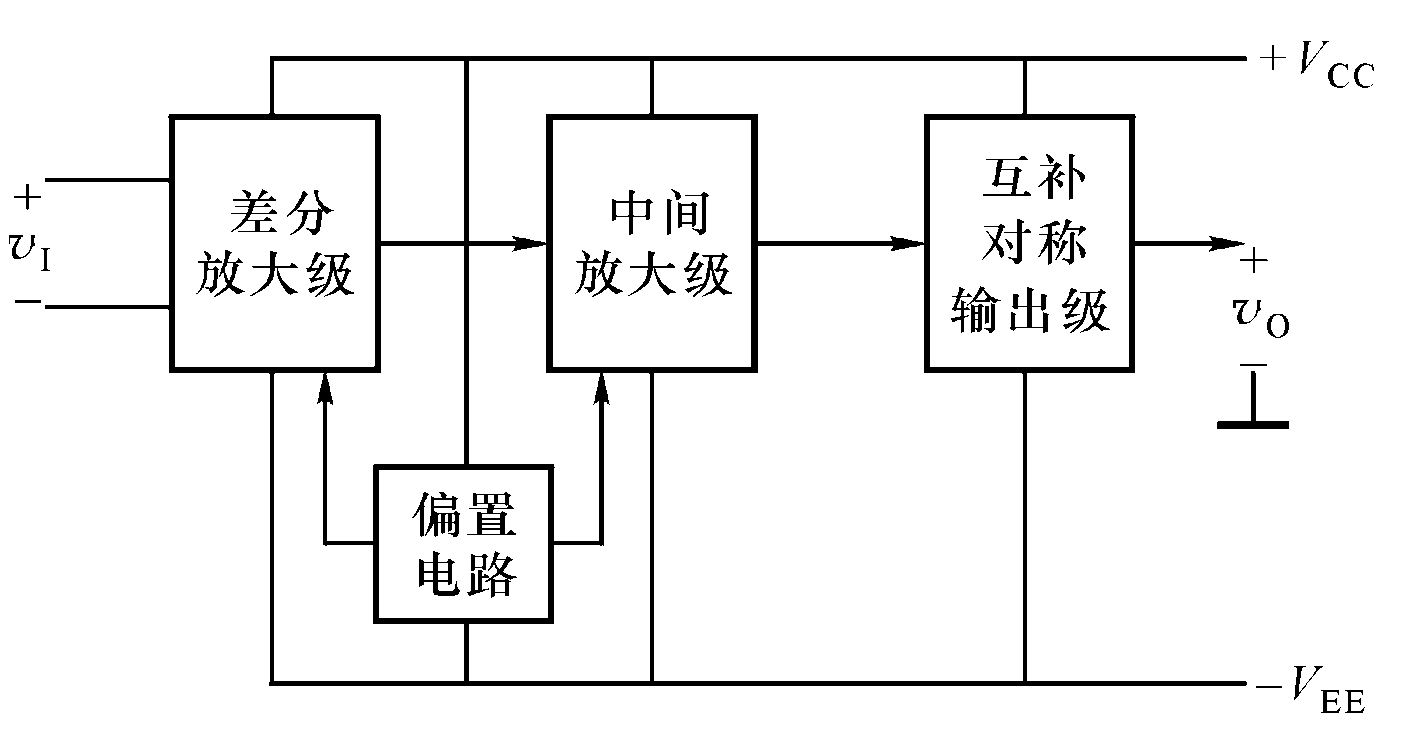各部分作用：输入级采用差分放大电路 -> 低温漂，高共模抑制比和高输入电阻

中间级采用CE(CS)电路 -> 高电压增益

输出级采用互补对称式射极跟随器结构 -> 低输出电阻，较强带负载能力

集成运放的电路符号

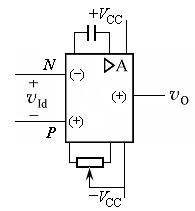
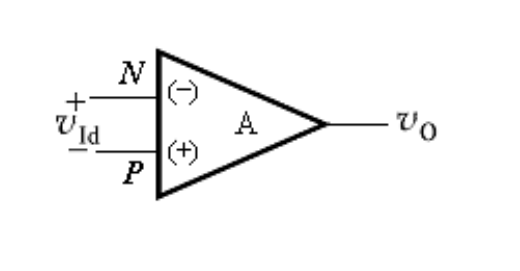
反相输入端：输入信号与输出信号相位反相
同相输入端：输入信号与输出信号相位同相

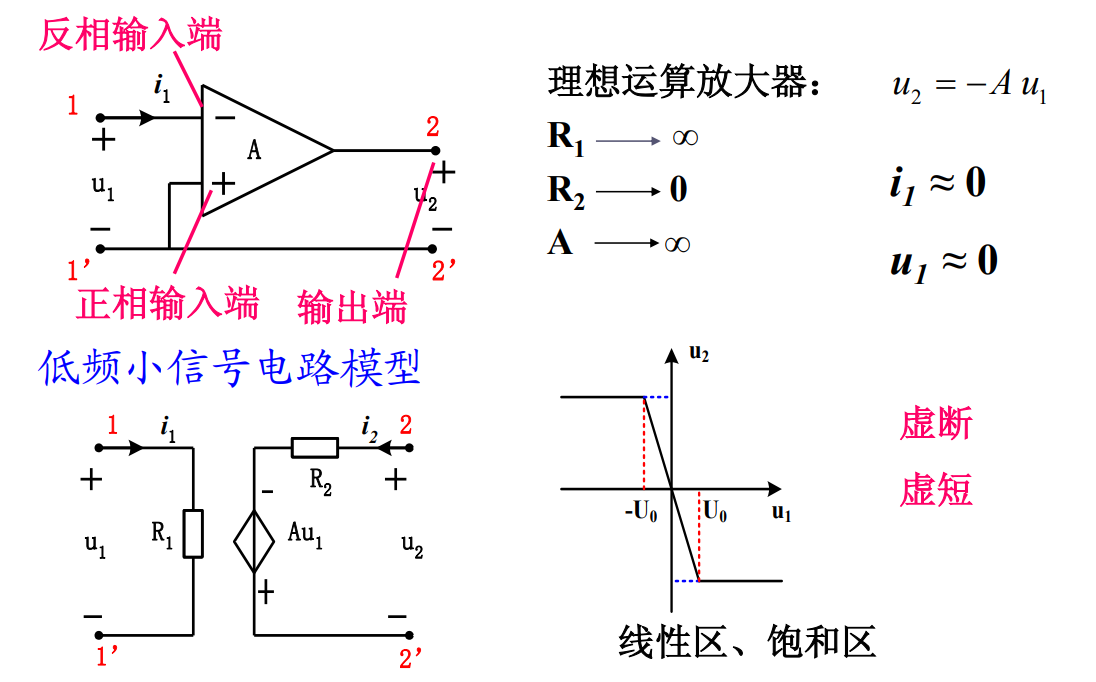
模型

具有“二高一低”特性。即高电压增益、高输入电阻、低输出电阻的多级直接耦合放大器。
在理想条件下，集成运算放大器可以等效成一个电压控制电压源（VCVS）。

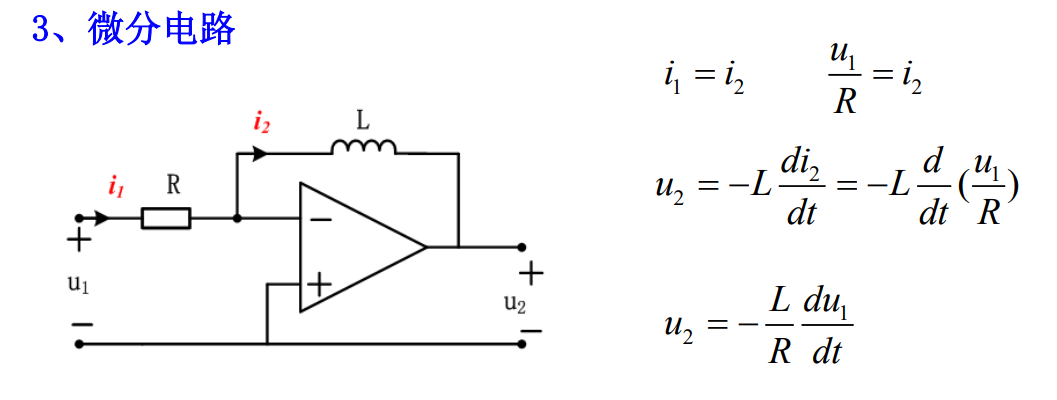
1.7.2 回转器

能把一个端口的电流回转成另一个端口的电压或把一个端口的电压回转成另一个端口的电流的器件。

基本方程

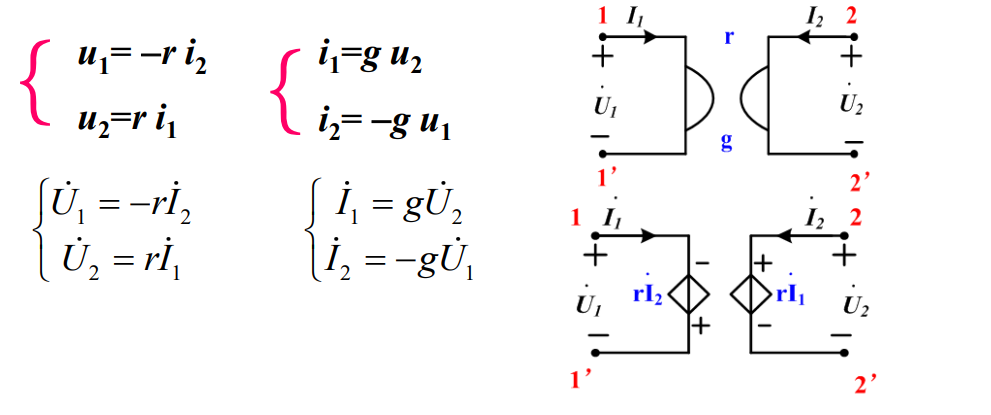
特点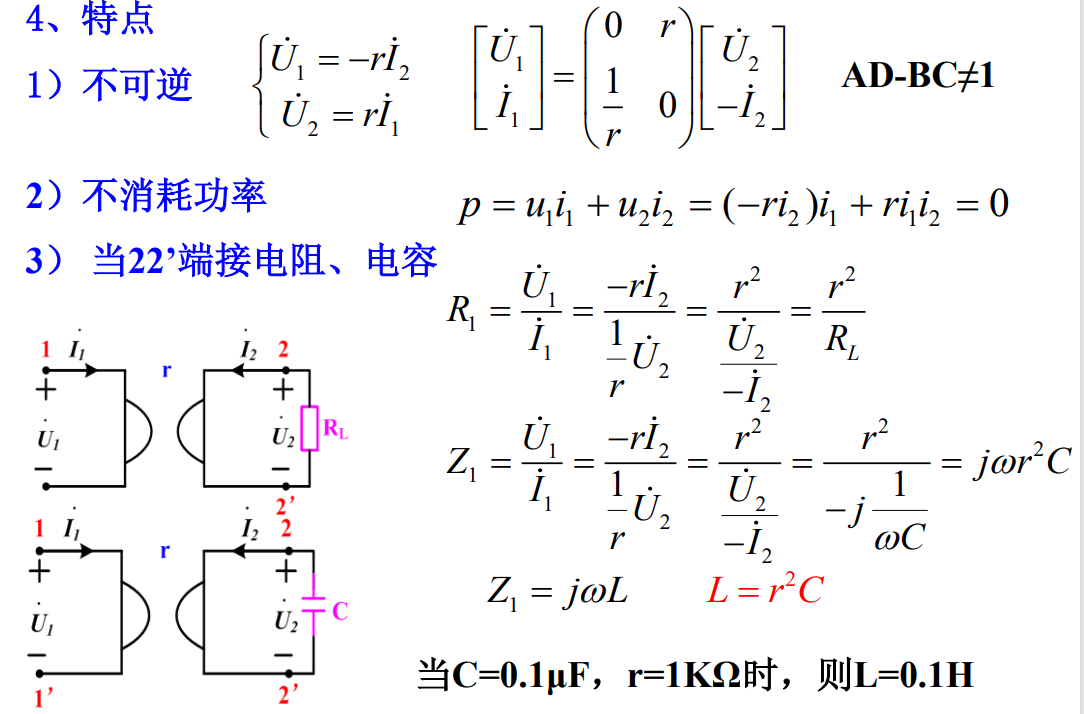

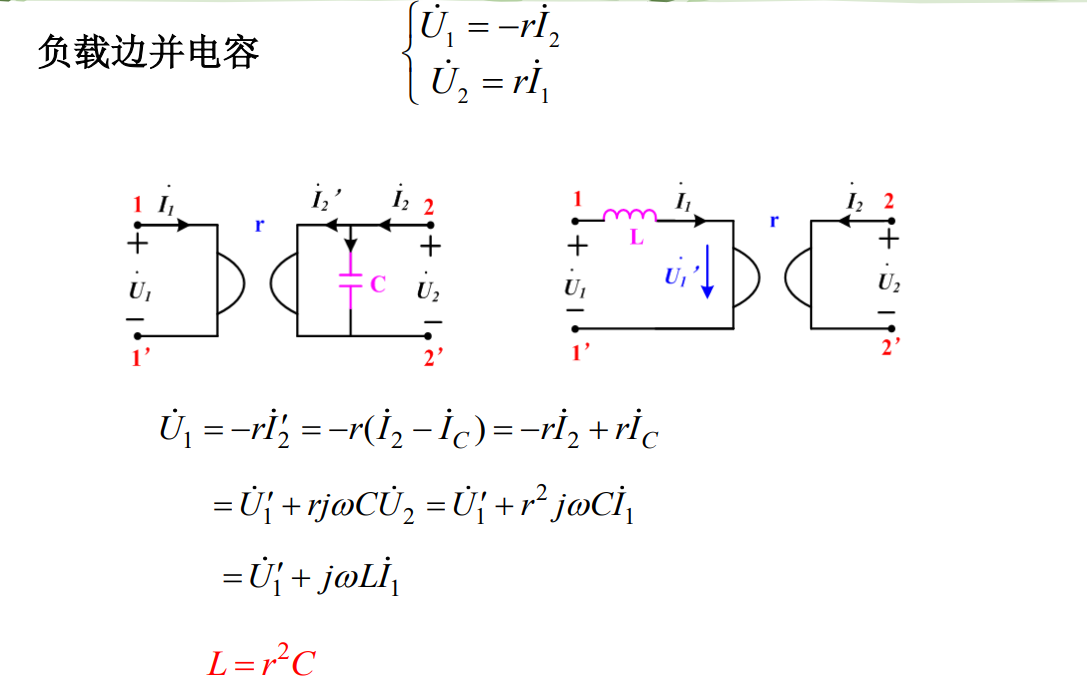
负载变换器

能把一个阻抗或元件参数按一定比例进行变换并改变其符号的双口器件。

1.7.3 负阻变换器

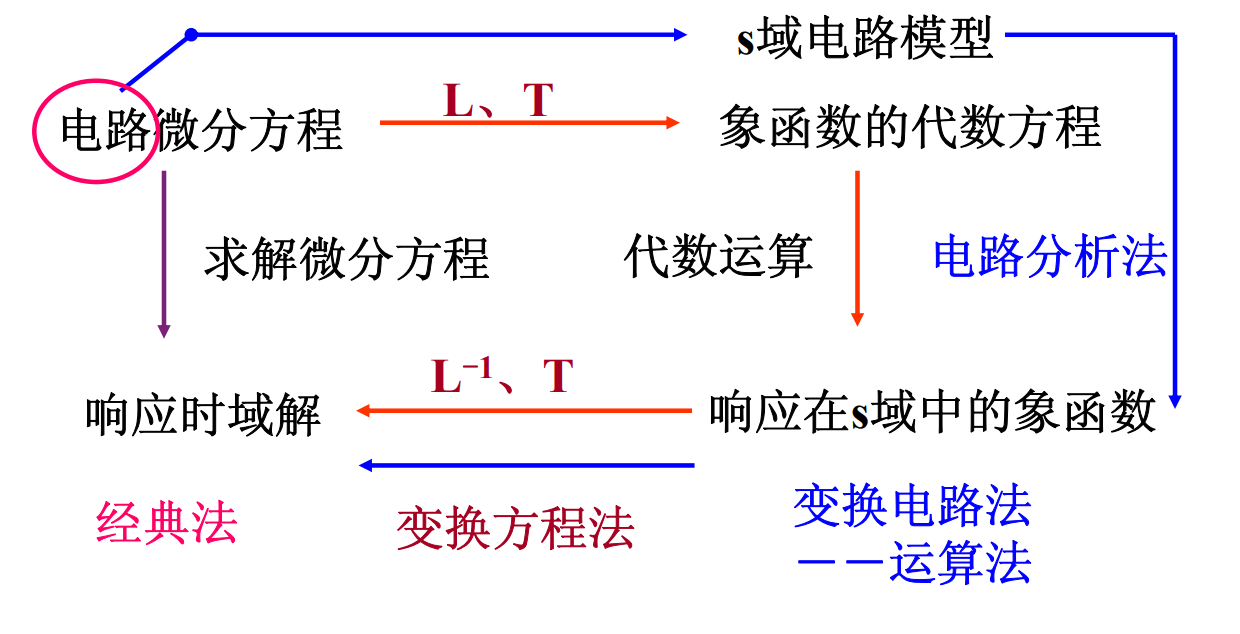
2 拉氏变换法分析电路

2.1 变换方程法

求出时的初值；
列出后的微分方程；
对微分方程进行拉氏变换；
求出响应的象函数；
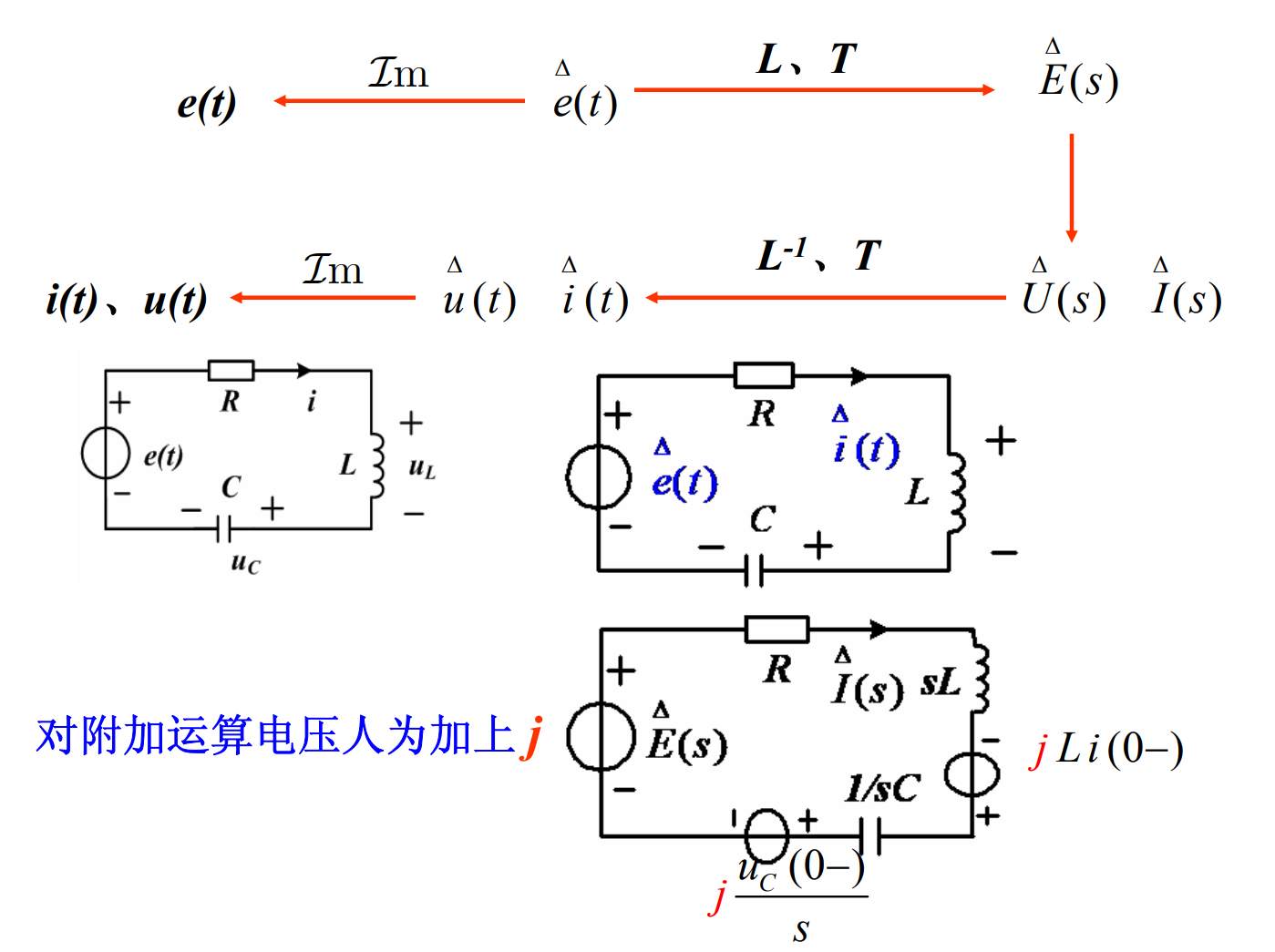
利用拉氏反变换求时域响应。 ### 2.2 变换电路法－－运算法
求出储能元件在时刻的初值；
画出运算电路模型； ( 将激励源的激励函数作拉氏变换; 元件用运算电路模型表示；电路变量用象函数表示 )
套用所有的方法、定理求解响应的象函数；
利用拉氏反变换得到响应的时域解

复频域中（s域中）的电路元件模型:

2.2.1 电阻R

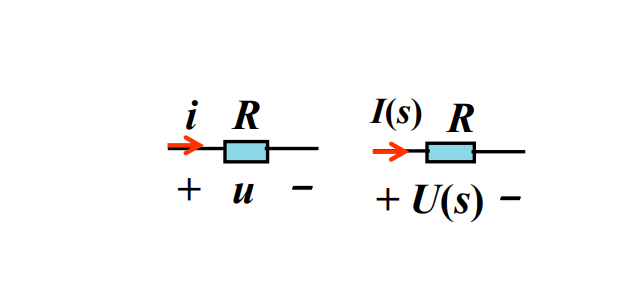
2.2.2 电容C

（1）称为复频域中的容抗 运算容抗

（2）附加运算电压方向

（3）两项合成

2.2.3 电感L

（1）称为复频域中的感抗 运算感抗

（2）附加运算电压方向

（3）两项合成

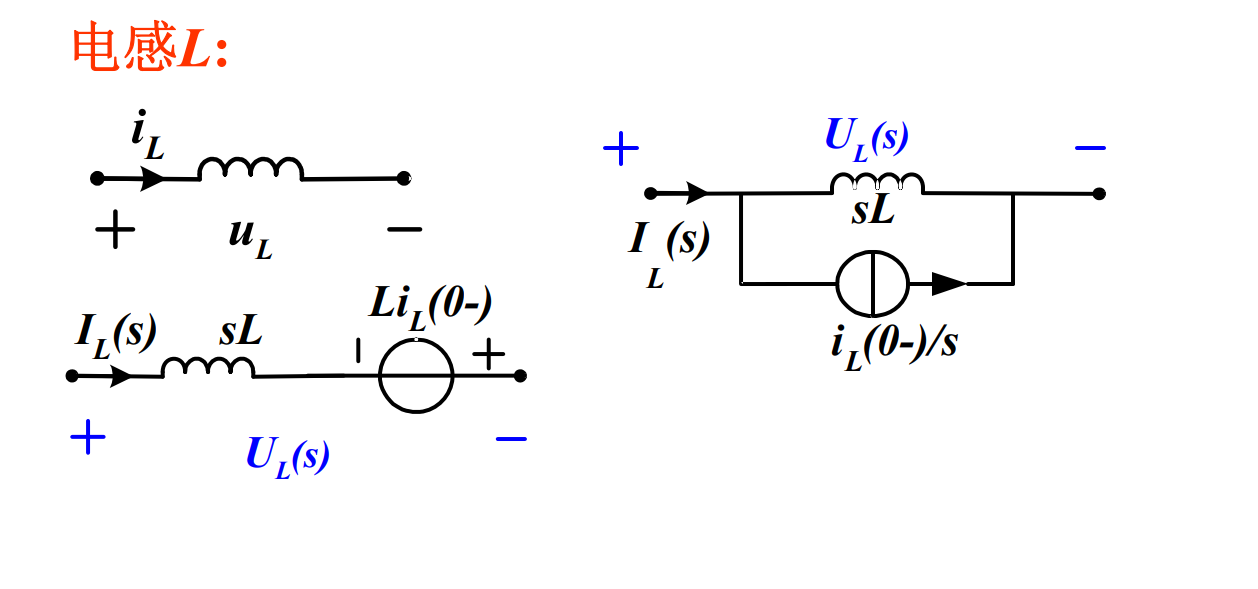
2.2.4 互感线圈

2.2.5 受控源

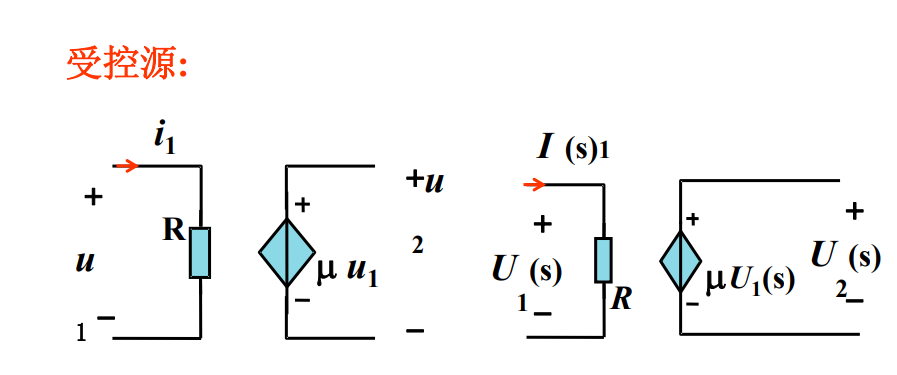
2.2.6 运算电路的建立

电路定律的运算形式：
元件 -> s域中元件模型->运算阻抗、运算导纳、附加运算电压运算形式欧姆定理与直流电路、正弦交流电路（相量形式）一致
KCL、KVL运算形式与直流电路、正弦交流电路（相量形式）一致

在s（复频域）域中，可以套用各种电路的求解办法、定理

运算电路： 元件用运算模型表示，激励用象函数表示，电路变量用象函数表示

只用初始条件，运用运算法求解，跳变情况自动包含在响应中；电路概念强调不够；
在s域中，可以充分运用各种电路的求解方法和定理；
当激励为一般正弦交流函数时，求解计算复杂

$构建记$

3 网络函数

3.1 网络函数定义

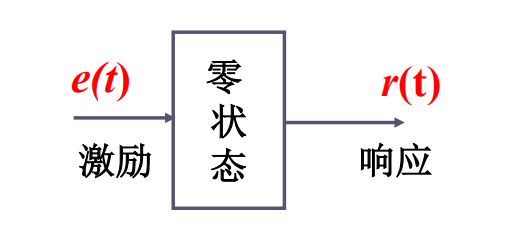
含有一个单一激励源的电路，其零状态响应 r(t) 的象函数 R(S)与该激励 e(t) 的象函数 E(S)之比，称为网络函数，记为：H(S)

网络函数是信号处理和控制系统中一个十分重要的概念, 网络函数完全决定了系统的输出响应特性和系统的稳定性.

3.2 网络函数形式

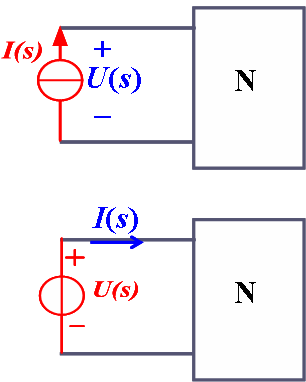
1. 策动点（驱动点）函数: 响应与激励处在同一端口 - 策动点阻抗 - 策动点导纳

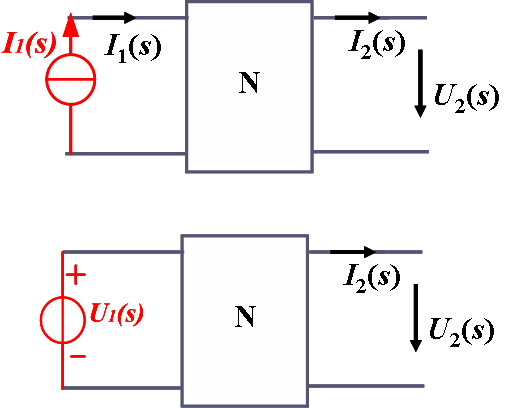
2. 转移函数(传递函数): 响应与激励处在不同端口 - 转移阻抗: - 转移电流比:
- 转移电压比:
- 转移导纳:

3.3 网络函数计算

（1）从微分方程求网络函数

的极点（分母的零点）就是特征方程的特征根

（2）从电路结构求网络函数

3.4 网络函数应用

由网络函数求取任意激励的零状态响应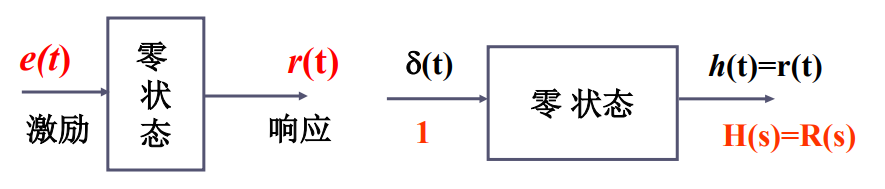

当时，即，，

就是冲激响应网络函数和冲激响应构成一对拉氏变换对

3.5 网络函数与稳定系统的稳态响应的关系

#TODO

Hole Black's Blog